ML - Regression

Regression

Machine Learning

机器学习的意义就在于让机器具备找一个函数（function）的能力

Different types of Functions

Regression

如果要找的函数输出的值是一个数值，即一个标量（scalar），那这样的机器学习就是线性回归的模型（Regression）

Classification

Classification主要是要机器做选择题，由人类事先准备好一些选项，类似于黑盒测试的原理，最后只需要机器给出选择这几个选项里面的哪一个即可，常见的如垃圾邮件的判定（YES/NO）

Alpha go本来也是一个分类问题，只是这个分类问题选项比较多，有19x19个选项（棋盘的大小），需要选出下一步应该落子的位置

Structured Learning

在回归问题与分类问题以外，我们还需要另外一种更复杂的机器学习，要产生一个具有结构的物体，比如需要机器去画一张图，写一篇文章，这种叫机器产生有结构的东西的问题，也就是说机器学习到了这一步，就需要去学习如何去创作一些东西。

Case Study

知道了机器学习就是需要去找一个函数，那我们就需要想想应该如何才能找到这个函数。拿某视频播放平台youtube的视频播放量来说，我们应该可以找到一个函数，输入我们前几天视频播放量或浏览量的数据，输出某一天这个视频总的观看次数，这里要先能够做到一个函数的大致数据和原数据拟合，再去考虑是否可以预测出未来的播放量。

而机器学习找到这个函数的过程，应当分为如下三步

1. Function with Unknown Parameters

第一步是需要我们写出一个带有未知参数的的函数，也就是说要写一个函数F，关于这个函数最初的形式，需要我们自己去进行推测，然后再拿推测的函数去测试，比如在这次，我们先写为如下的形式：
$y=b+w \ast x_1$ ①

1. y是我们准备去预测的value，此时我们准备预测的是今天此频道总的观看次数
2. $x_1$是这个频道前一天总的观看次数
3. b与w均为未知的参数，这是需要我们在函数中去找出来的，我们目前还不知道w与b应该为多少，只能做到猜测

在函数①中，b与w是未知的，是Unknown Parameter， 称为未知的参数，而这个parameter一般就叫做Model，所以我们常常听到有人说模型Model，这个在机器学习里面就是一个带有未知参数的函数。

而$x_1$是这个function里面我们已知的，是来自于YouTube后台的资讯，已经知道的某一天总人数是多少，这个叫做feature，而w与b是我们不知道的，是未知参数，在这里也给这俩哥们给个名字，与feature相乘的未知参数w，我们叫他weight，直接相加的叫Bias

2. Define Loss from Traing Data

第二部是要定义一个叫做loss的东西，它也是一个function，而这个function的输入是model里面的参数，我们的model是函数①，而b与w是未知的，是我们需要去找出来的。而loss这个function的输入就是b和w，输入是model里面的parameter，而这个loss输出的值就代表了把这一组未知的参数设定为某一个具体的数值的时候，这个数值到底是好还是不好

而这个loss的计算应当源自于训练资料，在这个问题里面，我们的训练资料是此频道过去的点阅次数。

我们把2017年1月1日的点阅次数，带入这一个函数里面，我们已经说我们想要知道，b设定为0.5k，w设定为1的时候，这个函数的结果是否优秀，当b设定为0.5k，w设定为1的时候，我们拿来预测的这个函数，是y等于0.5k加一倍的$x_1$，那我们就把$x_1$代为4.8k，看它预测出来的结果是多少，这时候不管是输入的数据还是输出的数据其实都是我们已知的，所以这时候可以拿着预测出来的数据和真正的结果比对一下，看看他们的差距有多大。比如在本例中，这个函数预估的结果是5.3k，而真正的结果是4.9k，那这个真实的值叫做label，它是高估点阅人数，因此我们可以计算一下这个差距是多少（即估测的值与真实的值的差距）估测的值用y表示，真实的值用$\hat y$来表示，那就可以计算一下这个差距，计算一下二者之间的差距，得到一个$e_1$，代表估测的值与真实的值之间的差距，
我们也可以把y与$\hat y$直接相减，取绝对值，算出来的值为0.4k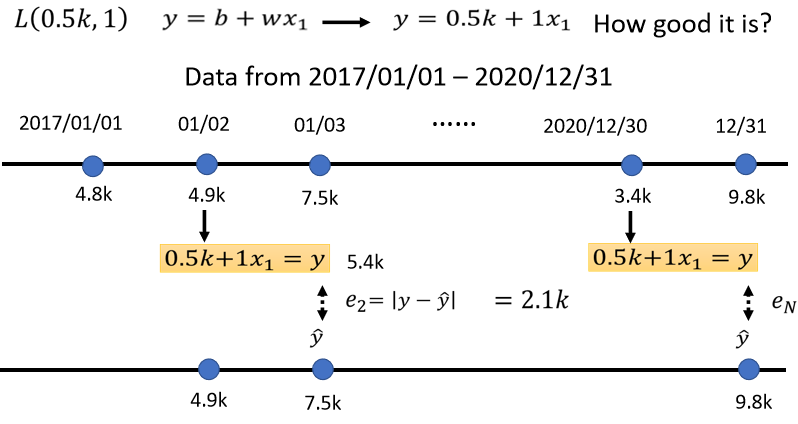

现在我们并不是只能用1月1号来预测1月2号的值，我们可以用1月2号的值，来预测1月3号的值，如果现在的函数是$y=0.5k+x_1$，那么再根据1月2号的点阅次数，再预测1月3号的点阅次数，值变更为了5.4k，以$x_1$代4.9k，乘1再加0.5k等于5.4k，接下来计算这个5.4k，跟真正的答案（label）之间的差距是7.5k，如此看来则是低估了这个频道，在1月3号的时候点阅次数才可以算出$e_2$，这个$e_2$是y与$\hat y$之间的差距，算出来是2.1k，那么用同一个方法，你就可以算出来这三年以来每一天的预测的误差，假设今天的function是$y=0.5k+x_1$，那么这三年来的每一天的误差，都可以计算出来，每一天的误差都可以给我们一个e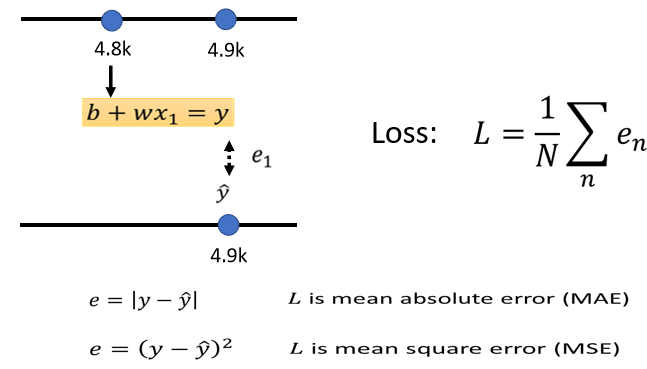

接下来要做的就是把每一天的误差都加起来，然后取一个平均值，这个大N代表我们训练资料的个数，就是三年来的训练资料，即365x3，算出一个L(oss)，这是每一笔训练资料的误差，这个e相加以后的结果就是我们的loss

L越大，代表我们现在这一组参数越不好，L越小越好

估测的值跟实际的值之间的差距，其实也有不同的计算方法，在刚刚的例子里面，我们计算的是y与$\hat y$之间的绝对值差距从而得到L，这样得到的loss叫做mean absolute error，简写为MAE，如果你今天的e是用y与$\hat y$相减的平方算出来的，这个叫mean square error，又叫MSE，这两者有着非常微妙的差别。如果选择MAE作为计算误差的方式，那么就是把所有的误差加起来就可以得到Loss，要选择MSE也是同样可以完成这个工作i的。另外，如果y和$\hat y$都是几率分布的话，这个时候可能需要选择Cross-entropy，这个我们之后再学习。

Error Surface

刚刚所举到的例子都不是真正的例子，以下的数字才是真实的例子，是频道真实的后台数据，现在我们可以动手实践了，我们可以调整不同的w，可以调整不同的b，求取各种w和b组合起来以后，为每一种不同的组合计算其Loss，从而画出如下的一个等高线图：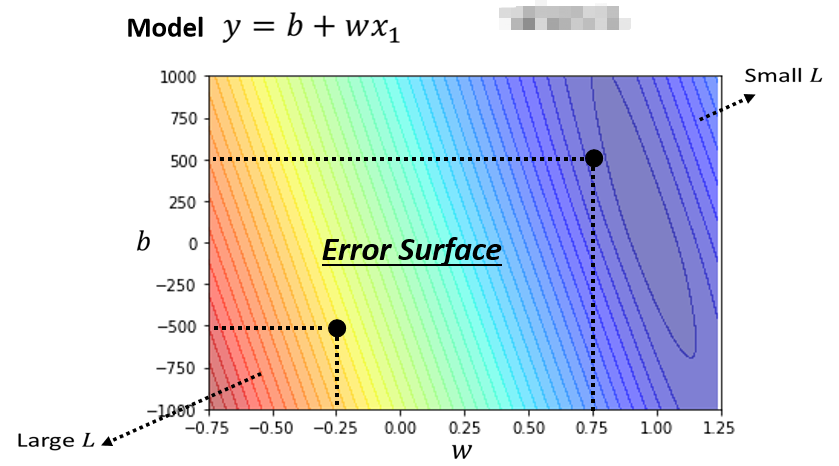

在这个等高线图上面，越偏红色系，代表计算出来的loss越大，就代表这一组w与b越差，如果越偏蓝色，就代表loss越小，也就是说这一组参数就越好，使用最好的一组w和b，放在我们的function和model里面，预测结果就会越精准。像这样的等高线图，你用不同的参数去计算它的loss，画出来的等高线图，就叫做Error Surface，这是机器学习的第二步

3. Optimization

接下来进入机器学习的第三步，我们需要解一个最佳化的问题，也就是说我们要找一个w和b（Unknown Parameter），看具体带入哪一个数值，可以让我们的L的值最小，这个值就是我们所要的w与b，我们称为w*和b*，代表说他们是最好的一组w和b，可以让loss的值最小

在这里我们用到的Optimization方法，叫做Gradient Descent。为了简化起见，我们先假设我们未知的参数只有一个w，而没有b这个未知的参数。当我们给w带入不同的数值时，我们就会得到不同的loss，这一条曲线就是error surface，此时由于只有一个unknown parameter，所以它的数据是1D（维）的

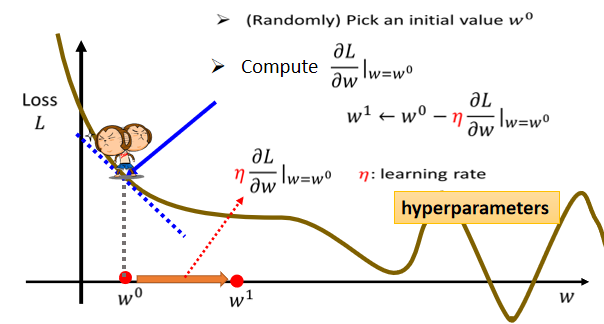
那么我们应该如何去找一个w。使得loss最小呢

1. 首先需要随机选取一个初始的点，记为$w_0$，这个初始的点往往就是随机的，只需要随机选定一个点即可。
2. 接下来就需要计算当w取$w_0$的时候，w这个参数对loss的微分是多少
   $\partial L/\partial w|(w=w^0)$，也就是求出在$w_0$这个位置error surface的切线的斜率，也就是上图中蓝色的虚线的斜率，如果这一条虚线的斜率是负的，就说明左边比较高，右边比较低
3. 如果发现左边比较高，右边比较低的话，我们就把w的值变大，从而使得loss变小，反之亦然

至于这一移到底要移多远，应当取决于以下两点

1. 首先要看这个地方的斜率有多大，这个地方斜率大的话，那么步伐就也要大一点，反之亦然。
2. 除此以外，在斜率之外，还有一个东西会影响步伐的大小，我们用$\eta$来表示，这个$\eta$叫做learning rate(学习速率)，这个是由我们自己设定的，如果偏大，那么每次参数更新的值就会变大，学习会比较快，如果偏小，改变就会比较小，学习的精度就会比较高。

在机器学习中，需要自己设定的东西，叫做hyperparameters

那么为什么loss可以出现负数呢？

loss这个函数是自定义的，我们说loss就是估测的值跟正确的值的差值，如果根据之前的定义，它确实不可能是负的，但是loss这个函数是由我们自己定义的，我们可以在运算时给它减掉100，那可能就有负的。总而言之，因为这个function是你自己决定的,所以它有可能是负的

继续上面的思路，把$w^0$向右移一步，这个新的位置我们记为$w^1$，这一步的步伐是$\eta$乘上微分的结果，用数学式推导如下：
$w^1 \gets w^0 - \eta \frac{\partial L}{\partial w}|(w=w^0)$
接下来就是反复进行这个操作，不断地移动w的位置，直到最后停下来

那么什么时候会停下来呢？

这里面有两种状况:

1. 第一种状况是你失去耐心了，用行话讲就是微分次数达到你自己的设定的上限了，那么到这儿也就不再更新了，这也是一个hyperparameter，由我们自己决定
2. 还有另外一种理想状态上的停止，就是当我们不断调整参数，到了某一个$w_n$的时候，算出来的值正好是0，而0乘上learning rate $\eta$还是0，所以参数就不会再移动位置，假设我们是这个理想状况，我们把$w^0$更新到$w^1$，再更新到$w^2$，直到最后更新到$w^t$卡住了，也就是说到这儿算出来的这个微分值是0了，那么参数的位置就不会再更新。

所以说，Gradient Descent并没有找到真正最好的解

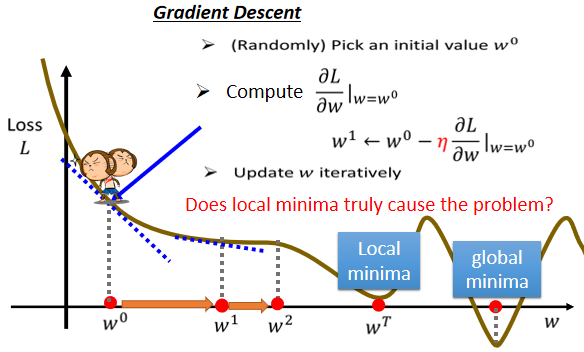
如上图中，如果把w设定在最右侧的红点位置，就可以让loss最小，但是按照我们的算法，如果Gradient Descent是从$w^0$开始的，那很有可能走到$w^T$处，训练就结束了

我们称右侧红点这个**可以让loss最小的地方为global minima**，而$w^T$这个地方叫做local minima，它的左右两边，都比这个地方的loss要高一点，但是它不是整个error surface上面的最低点，这个问题并不影响关键结果，在之后还会有讨论。

解决了一个参数的例子后，我们再回到最初的问题，我们对于视频播放量预测的模型有两个参数：w和b，那么有两个参数的时候，其实参照一个参数的问题，很容易就可以推导出两个参数应该如何去做。

1. 我们现在有两个参数， 都给它随机的初始值，也就是$w^0和b^0$
2. 计算w与loss的微分以及b对loss的微分，计算当$w=w^0$, $b=b^0$时，对应的微分。
   $\frac{\partial L}{\partial w}|(w=w^0, b=b^0)$,
   $\frac{\partial L}{\partial b}|(w=w^0, b=b^0)$
   计算结束以后，我们就可以以此去更新w和b，把$w^0$减掉learning rate，乘上微分的结果得到$w^1$，把$b^0$减掉learning rate，乘上微分的结果得到$b^1$
   $w^1 \gets w^0 - \eta \frac{\partial L}{\partial w}|(w=w^0, b=b^0)$,
   $b^1 \gets b^0 - \eta \frac{\partial L}{\partial b}|(w=w^0, b=b^0)$

Conclude

在这个问题里面，算出一个微分的值，就可以决定新的方向，把w与b更新的方向结合起来，就是一个向量，就是如图所示的红色箭头，就可以从一个位置移动到另一个位置。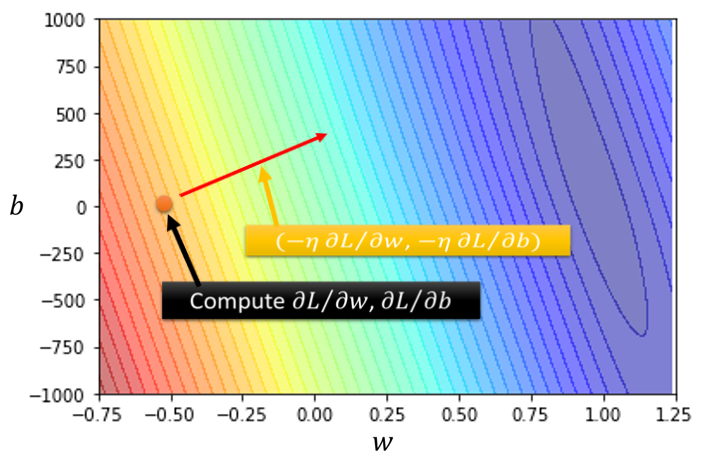

然后再计算一次，再决定要走什么样的方向，把这个微分的值乘上learning rate，再乘上负号，你就知道红色的箭头指向哪里，从而移动w与b的位置，一直到最后找出一组相对最优的w与b

这个例子最终使用Gradient Descent计算出真正的数据后，最好的w是0.97，最好的b是0.1k，参考预测与实际的观看人数对比，误差大约在500人左右。

Linear Model

虽然相对最优的w和b已经找出来了，他们可以让loss小到0.48k，但是这样也并不是一个令人满意的结果，因为上面的步骤合起来叫做训练，训练阶段其实是以我们已经知道的2017到2020年每天的观看此处，所以更多的只是在现有数据上（假装不知道罢了）做的一个分析

但是我们模型的最终目的是去预测我们不知道的未来的观看次数是多少，所以我们要用拿到的这个函数去预测未来的观看次数去计算误差，如图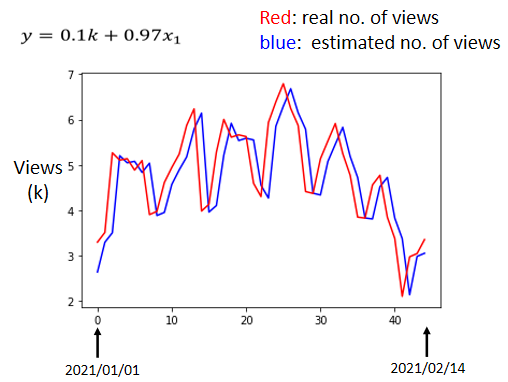

我们来根据图片分析一下结果：

1. 横轴代表的是时间。所以0这个点，最左边的点，代表的是2021年1月1号，最右边的点，代表的是2021年2月14号。
2. 纵轴就是观看的人次。这里用千人作为单位。
3. 红色的线就是真实的观看人次。
4. 蓝色的线是机器学习预测的人次。

我们可以很明显的发现，蓝色的线没有什么神奇的地方，几乎就是红色的线往右平移了一天而已。其中比较有意思的一点是这个模型每隔七天有一个循环，所以说如果我们的模型只参考七天的资料，说不定还会预测的更准，所以我们需要修改一下我们的模型，通常一个模型的修改，往往也来自于你对这个问题的理解，称为Domain Knowledge。

所以，此时针对我们一开始乱写的（这可不是乱写的啊）$y=b+wx_1$得出的结论并没有做的特别好，我们观察模型得到的结论是每七天有一个循环，所以我们可以考虑一个新的模型$y=b+ \sum_{j=1}^{7}w_jx_j$，x的下表j代表是第几天前，一直考虑到七天以前，这些资料，都乘上不同的weight，加起来，再加上bias，得到新的预测的结果。

如果这就是我们的model，我们得到的结果中loss的值降低到了0.38k。这里的每一个w和b，都会用gradient descent算出其最佳的值。(这里机器没有直接选用七天前的数据)

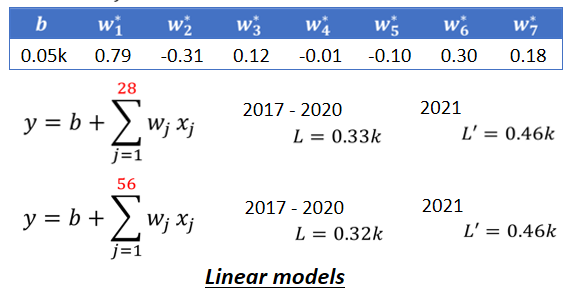
其逻辑就是前一天与要预测的隔天的数值的关系很大，所以$w_1*$就是0.79，前三天是0.12，前六天是0.3，前七天是0.18，所以这些所有最佳的值让model得到的loss可以保持在0.38k上

除此以外还可以考虑选用28天（一个月）的数据，去预测隔天的观看人数，这样得出来的loss是0.33k，如果考虑56天，loss再好一点，是0.32k。看起来，我们考虑再更多天也无法使其进步了，看来考虑天数这件事，已经到了一个极限。但是这里的模型都是一个x（称为feature）乘上一个weight，再加上一个bias就得到预测的结果，这样的模型都有一个共同的名字，叫做Linear model，下面就会探讨如何把Linear model做得更好。